Comparaison de deux variances - Test de conformité - Calculs et Décision
On calcule la valeur :
Sous l’hypothèse
:
-
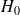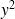suit la loi du
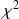à
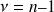ddl
Conditions d'application
-
La distribution des données dans la Population doit être normale
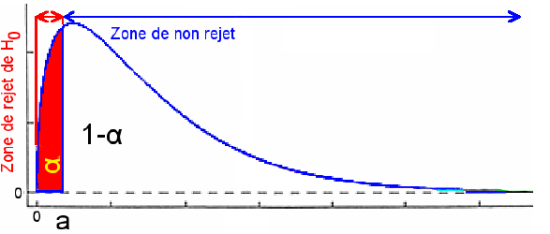
Choix du risque :
-
Risque de première espèce
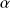(erreur commise lorsqu’on rejette
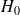à tort). -
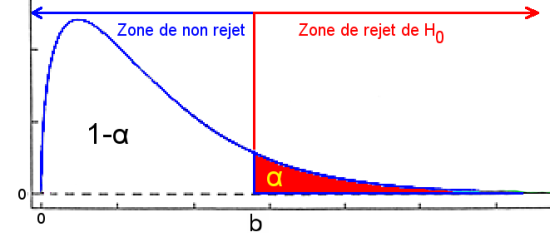
On cherche la valeur seuil
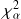dans la table du
.
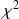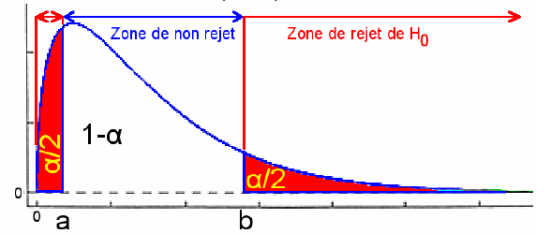
Si
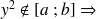rejet de
au risque
:
-
la variance expérimentale n'est pas conforme à la variance théorique : la variance expérimentale est différente de celle de la population.
-
Recherche du degré de signification p (recherche du risque
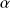le plus petit possible pour conclure au rejet de
)
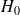Sinon rien ne permet de dire que
-
la variance expérimentale n'est pas conforme à la variance de la population
n’est pas rejetée.
Si
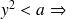rejet de
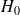au risque
:
-
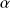la variance expérimentale n'est pas conforme à la variance théorique : la variance expérimentale est inférieure à celle de la population.
-
Recherche du degré de signification p (recherche du risque
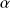le plus petit possible pour conclure au rejet de
)
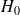Sinon rien ne permet de dire que
-
la variance expérimentale n'est pas conforme (égale ou plus grande) à la variance de la population
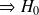n’est pas rejetée.
Si
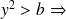rejet de
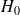au risque
:
-
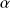la variance expérimentale n'est pas conforme à la variance théorique : la variance expérimentale est supérieure à celle de la population.
-
Recherche du degré de signification p (recherche du risque
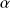le plus petit possible pour conclure au rejet de
)
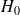Sinon rien ne permet de dire que
-
la variance expérimentale n'est pas conforme (égale ou plus petite) à la variance de la population
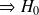n’est pas rejetée.
