Comparaison de deux variances - Test d'homogénéité - Décision
Sous l'hypothèse
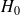 :
:
-
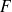 suit la loi de Snédécor à
suit la loi de Snédécor à
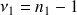 et
et
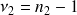 ddl
ddl
Conditions d'application :
-
La distribution des données dans la Population doit être normale
-
Les échantillons doivent être indépendants
Choix du risque :
-
Risque de première espèce
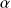 (erreur commise lorsqu’on rejette
(erreur commise lorsqu’on rejette
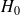 à tort).
à tort). -
On cherche la valeur seuil
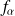 dans la table de Snédécor.
dans la table de Snédécor.
Dans le cas d'un test bilatéral, on cherchera également la valeur seuil
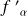 . Cette valeur seuil permet de tester le cas où
. Cette valeur seuil permet de tester le cas où
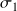 est inférieure à
est inférieure à
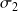 .
.
En pratique, il suffit, dans le cas où
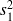 est inférieure à
est inférieure à
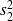 , d'inverser le rapport
, d'inverser le rapport
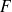 afin qu'il soit toujours supérieur à 1 :
afin qu'il soit toujours supérieur à 1 :
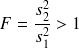
On cherchera alors dans la table de Snédécor la valeur seuil
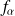 pour
pour
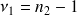 et
et
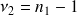 ddl.
ddl.
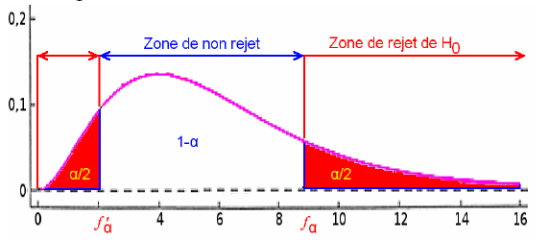
Si
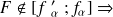 rejet de
rejet de
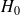 au risque
au risque
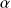 :
:
-
les variances expérimentales sont significativement différentes : les variances des populations
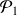 et
et
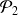 ne sont pas égales.
ne sont pas égales. -
Recherche du degré de signification p (recherche du risque
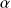 le plus petit possible pour conclure au rejet de
le plus petit possible pour conclure au rejet de
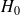 )
)
Sinon rien ne permet de dire que
-
les variances des populations ne sont pas égales
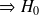 n’est pas rejetée.
n’est pas rejetée.
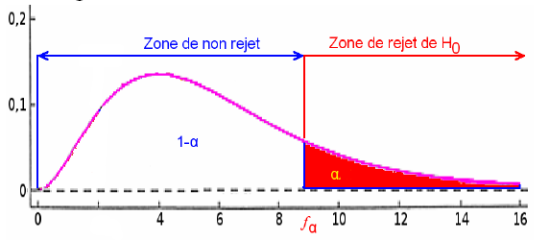
Si
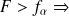 rejet de
rejet de
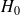 au risque
au risque
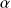 :
:
-
les variances expérimentales sont significativement différentes : la variance de la population présente au numérateur du rapport
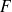 est supérieure à celle présente au dénominateur.
est supérieure à celle présente au dénominateur. -
Recherche du degré de signification p (recherche du risque
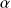 le plus petit possible pour conclure au rejet de
le plus petit possible pour conclure au rejet de
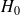 )
)
Sinon rien ne permet de dire que
-
les variances des populations ne sont pas égales (variance au numérateur égale ou inférieure à celle présente au dénominateur)
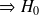 n’est pas rejetée.
n’est pas rejetée.
