Comparaison de plusieurs variances - Test d'homogénéité - Méthode approximative
Empiriquement, on peut essayer d'avoir une idée approximative de la signification des différences existantes entre les variances en réalisant un test qui ressemble à celui de Hartley mais qui n'est cependant pas très correct.
L'intérêt de réaliser ce test est qu'il est plus rapide à réaliser que le test de Bartlett et qu'il permet d'utiliser des échantillons de tailles inégales (impossible dans le cas du test de Hartley).
On va donc calculer le rapport suivant :
Sous l'hypothèse
:
-
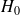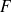suit la distribution de Snédécor à
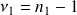et
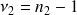ddloù
-
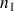est l'effectif de l'échantillon possédant la variances la plus élevée (
) -
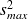et
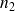est l'effectif de l'échantillon possédant la variances la plus petite (
)
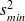Conditions d'application :
-
La distribution des données dans la Population doit être normale (?)
-
Les échantillons doivent être indépendants (?)
Choix du risque :
-
Risque de première espèce
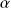(erreur commise lorsqu’on rejette
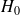à tort). -
On cherche la valeur seuil
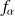dans la table de Snédécor.
Si
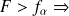rejet de
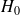au risque
:
-
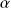les variances expérimentales sont significativement différentes : les variances des populations ne sont pas toutes égales (puisque les deux variances extrêmes sont différentes).
-
Recherche du degré de signification p (recherche du risque
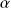le plus petit possible pour conclure au rejet de
)
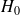Sinon rien ne permet de dire que
-
les variances des populations ne sont pas égales
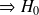n’est pas rejetée.
Cette méthode ne devrait être mise en oeuvre qu'en première approche et devrait par conséquent être complétée par un test plus robuste.
Il est clair que si elle est utilisée, c'est principalement pour éviter d'en utiliser une autre plus lourde...
