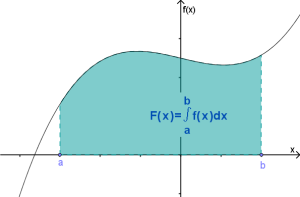
Intégrales et primitives
Comme dans le point précédent, il est nécessaire d'effectuer quelques rappels mathématiques : formules de calculs, intégrales, primitives et propriétés.
Soit
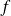une fonction réelle. L'aire sous la courbe sur l'intervalle
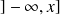varie lorsqu'on fait varier
de
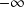à
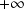. Cette aire est une fonction
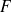de
, appelée fonction primitive de
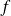. Elle est définie par :
Noter l'utilisation de la variable d'intégration
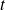. On peut utiliser n'importe quel nom de variable (il s'agit d'une variable muette), différent de la borne d'intégration
.
-
Si , alors
Donc
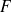se déduit de
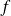par intégration, et
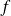se déduit de
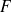par dérivation.
On écrit souvent en omettant les bornes d'intégration.
