Définitions

• Expérience composée d’une action pouvant engendrer plusieurs résultats possibles.

• L’ensemble de tous les résultats possibles peut être décrit.

• Le résultat ne peut pas être prédit avec certitude.

• Chaque résultat possible a une probabilité de réalisation.

• Événement = sous-ensemble de l’ensemble de tous les résultats.

• Par exemple : étudions la couleur des yeux et la taille des ailes des drosophiles. On distingue :

  • l'événement "avoir des ailes normales" arbitrairement noté A.

  • l'événement "avoir des yeux rouges" arbitrairement noté B.

• L'événement est l’opposé de l’événement A, c'est-à-dire "avoir des ailes anormales".

• De même, l'événement contraire de B est noté et représente le fait d‘ "avoir des yeux non rouge".

• Variable dont la valeur est déterminée en fonction du résultat d’une expérience aléatoire.

• Discrète : si les valeurs qu’elle prend est un ensemble fini ou infini dénombrable.

• Continue : si les valeurs qu’elle prend est un ensemble infini non dénombrable.

• Convention de notation : désignée par une lettre majuscule de l’alphabet.

• Modèle représentant au mieux une distribution de fréquences d’une variable aléatoire.

• Discrète : définie par sa fonction de probabilité P(x) ou sa fonction de répartition F(x).

• Continue : définie par sa fonction de densité de probabilités f(x) ou sa fonction de répartition F(x).

• Fonction qui associe à chaque valeur d’une variable aléatoire sa probabilité.

• Notation pour une variable aléatoire discrète X : .

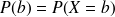Fonction qui détermine la probabilité qu’une variable aléatoire prenne une valeur dans un intervalle fixé.

Notation pour une variable aléatoire continue X : soit f une fonction non négative définie sur , pour tout intervalle ]a ; b[ :

• Notation : F(x)

• Fonction calculant la probabilité pour que la variable aléatoire prenne une valeur inférieure ou égale à x