Loi normale (de Gauss ou de Laplace-Gauss)
-
Soit X la variable aléatoire continue de paramètres
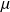et
:
-
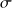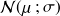
Fonction de densité de probabilités pour une expérience aléatoire :
-
Espérance mathématique :
-
Variance :
MéthodeApproximation d'une loi binomiale par une loi normale
-
Si n est grand et p pas trop voisin de 0 et de 1 :
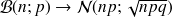
avec
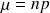et
-
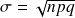
En pratique, l’approximation est satisfaisante quand :
-
n ≥ 30
-
np ≥ 5
-
nq ≥ 5
-
ComplémentPropriétés : Allures de la courbe
-
La loi normale, notée
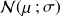, est symétrique par rapport à la droite d'abscisse
.
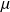Exemples (avec le même
) :
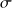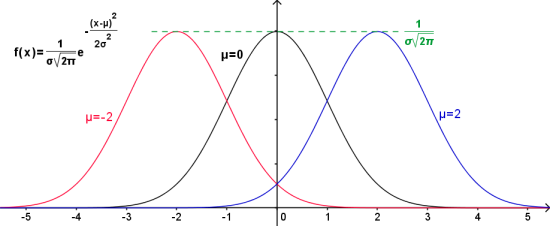
Figure 19 : Courbes de Gauss en fonction de µ (même écart type)[Zoom...]
-
La hauteur de la courbe dépend de la valeur de
.
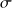Exemples :
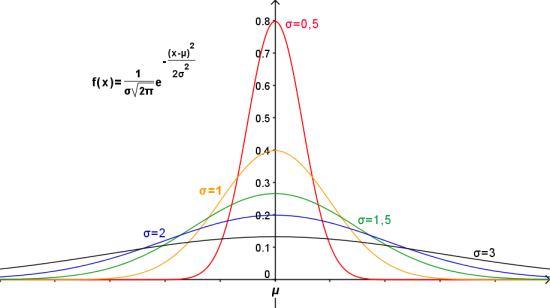
Figure 20 : Courbes de Gauss en fonction de σ (même moyenne)[Zoom...]
