1.1.VA continue
1.1.1.Loi Normale (Laplace Gauss)
Cette loi de distribution théorique est celle que l'on rencontre le plus souvent en statistique car elle modélise bien un grand nombre de distributions observées. Cela tient au fait qu'elle s'applique, comme l'a précisé le mathématicien Emile Borel, lorsque les variations d'un phénomène sont la résultante de très nombreux facteurs agissant de manière indépendante et produisant des effets petits et du même ordre de grandeur. Ces facteurs sont appelés également causes aléatoires et se différencient des causes dites assignables qui sont peu nombreuses mais produisent des effets importants..
Fonction de densité de probabilité
D'un point de vue mathématique, la loi normale est associée à une fonction mathématique définie pour une variable continue x. L'équation de cette fonction est la suivante :
où µ et σ sont deux constantes.
Ramenée aux problèmes statistiques, la variable continue est une variable aléatoire notée X qui peut prendre, en théorie un ensemble infini de valeur réelles. Les deux constantes correspondent aux paramètres de position (moyenne µ) et de dispersion (variance σ 2 ou écart-type σ ) déjà décrits.
Cette fonction f(x) est également nommée fonction de densité de probabilité. Par définition, une fonction densité de fréquence est telle que l'intégrale de cette fonction sur son ensemble de définition est égale à 1.
La fonction densité de probabilité de la loi normale est donc entièrement définie par ses deux paramètres constants, µ et σ . Une loi normale de moyenne µ et d ‘écart type σ sera notée : N(µ, σ ) ou N(µ, σ 2) si l'on fait intervenir la variance.
La courbe représentant la fonction de densité de probabilité f(x) est caractérisée par son allure en forme de cloche comme le montre la figure suivante :
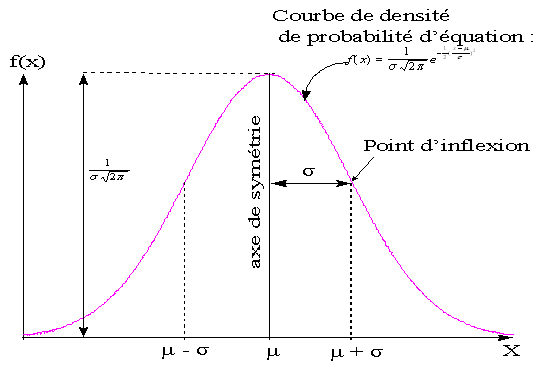
Cette courbe symétrique (axe de symétrie d'équation x=µ) présente un maximum au point d'abscisse m et d'ordonnée . On trouve une asymptote parallèle à l'axe des abscisses lorsque et deux points d'inflexion aux abscisses µ ± σ .
Il existe autant de courbes possibles que l'on peut définir de distributions théoriques, c'est à dire une infinité. La forme de la courbe est déterminée par les valeurs que l'on assigne aux constantes µ et σ .Pour une valeur constante de σ, la courbe sera d'autant plus aplatie que sera grand. Le fait de faire varier uniquement l'écart type génère ainsi une homothétie géométrique.
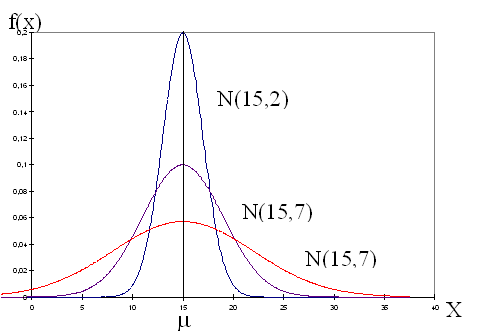
Lorsque l'on fait varier uniquement la moyenne, on obtient un ensemble de courbes qui subissent un effet de translation.
La variation simultanée des deux paramètres modifie la forme des courbes qui subissent la combinaison d'une homothétie et d'une translation.
Fonction de répartition
Comme nous l'avons vu, la fonction de densité de probabilité est telle que l'intégration de cette fonction sur l'ensemble des réels génère une valeur égale à 1. Cette opération d'intégration consiste à déterminer la surface sous la courbe (partie hachurée vers la droite sur la figure suivante). L'ensemble des cas favorables (défini par ) est alors confondu avec l'ensemble des valeurs possibles (Chaque valeur doit avoir la même probabilité d'être rencontrée ; on parle de cas possibles tous équiprobables ) que peut prendre la variable aléatoire X et la probabilité p( )=nombre de cas favorable/nombre de cas possibles est alors égale à 1.
Le rapport entre une portion d'aire sous la courbe (nombre de cas favorables) et la surface totale (nombre de cas possibles) peut lui varier entre les valeurs 0 et 1 ce qui correspond à l'intervalle qui contient les résultats de l'intégration de la fonction de densité de probabilité.
Le résultat de l'intégration entre 2 bornes x1 et x2 (ce qui correspond à la partie encadrée sur la figure suivante) est la probabilité que la variable aléatoire prenne ses valeurs dans cet intervalle.
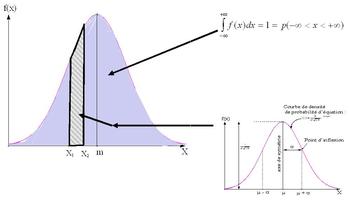
Ceci nous permet de définir la fonction de répartition de la variable aléatoire X qui donne l'ensemble des différents résultats possibles pour l'intégration de la fonction de densité de probabilité. On peut obtenir cet ensemble en calculant pour chaque valeur de X l'intégrale suivante : .
La courbe correspondant à la fonction de répartition (que l'on nommera F) a pour équation F(x1) = .
L'allure générale de cette courbe est représentée sur la figure suivante. On constate que les graduations de l'axe des abscisses dépend des constantes µ et σ . La probabilité d'obtenir une valeur supérieure ou inférieure à µ est égale à 0,5. On peut facilement à partir de cette courbe obtenir n'importe quelle probabilité. On constate par exemple que la probabilité d'avoir une valeur comprise entre égale à 0,95 c'est-à-dire la différence entre les ordonnées de valeur 0,975 et 0,025 correspondant respectivement aux probabilités et .
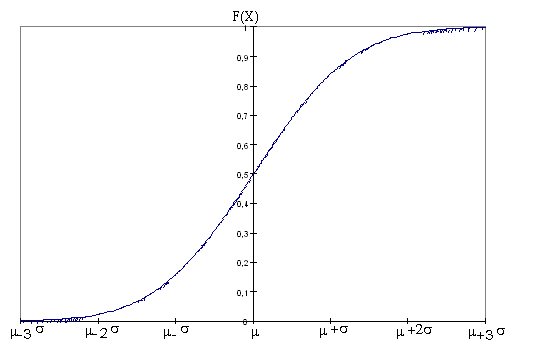
Variable normale centrée réduite
D'un point de vue pratique, il n'est pas aisé de manipuler autant de courbes différentes qui représente une même loi de distribution. On a donc cherché à se ramener à une loi de distribution n'ayant plus qu'une seule fonction de densité de probabilité et une seule fonction de répartition . Cela est possible en effectuant un changement de variable afin d'obtenir une nouvelle variable appelée variable centrée réduite qui ne dépend plus de µ et σ .
Ainsi, en remplaçant le terme x-µ par une variable X' (appelée variable centrée), il ressort que la position de toutes les courbes sera centrée sur l'abscisse de valeur nulle. En effet, cette nouvelle distribution théorique correspond à la distribution des écarts par rapport à la moyenne et l'on sait que la moyenne de ces écarts est nulle.
Il reste le problème de la valeur de l'écart type qui va influencer l'étalement des courbes. En utilisant un nouveau changement de variable à l'aide d'une variable que l'on appellera variable centrée réduite (ε ) ou fractiles de la loi normale, de formule , l'échelle des abscisses devient indépendante de l'unité de mesure. Cette variable est donc sans dimension et est indépendante du choix des unités.
L'équation de la fonction de densité de probabilité de la variable normale centrée réduite devient : .
La fonction de densité de probabilité de la variable centrée réduite présente les caractéristiques suivantes :
-
la courbe est symétrique par rapport à l'axe d'abscisse nulle
-
l'écart type est égal à 1
On est donc ramené, quelle que soit la distribution initiale, à une seule distribution dont nous pouvons calculer les probabilités cherchées.
EXEMPLE
Prenons l'exemple d'une distribution de moyenne m=15 et d'écart type σ =2 et calculons les probabilité suivantes :
p(x<12) ; p(x>18) ; p(14<x<18) ; p(x<16).
Si l'on se ramène à la distribution de la variable centrée réduite , les probabilités deviennent : p(x<12)= ; p(x>18)=p(ε >1,5) ; p(14<x<18)=p(-0,5<ε <1,5) ; p(x<16)=p(ε <0,5).
La lecture des probabilités peut se faire sur la courbe de répartition de la variable centrée réduite.
Ainsi =0,067
p(ε >1,5) = 0,067 (on pouvait déduire directement ce résultat puisque la distribution de la variable centrée réduite est symétrique p(ε >1,5) = )
p(-0,5<ε <1,5)=p(ε <1,5)-p(ε <-0,5)=0,933-0,69=0,243 (la probabilité p(ε <1,5) pouvait se déduire du résultat précédent par p(ε <1,5)=1-p(ε <-1,5)=1-p(ε >1,5)=1-0,067=0,933. p(ε <0,5)=0,31 (c'est également 1-p(ε <-0,5)=1-p(ε >0,5)).
La lecture des probabilités sur la courbe de la fonction de répartition est directe. En revanche, on trouve le plus souvent dans les livres, la table de la loi normale (voir annexes) qui donne le résultat de la fonction de répartition :
pour des valeur positives de ε
et des inégalités dans le sens p(ε <ε i)
On est donc amené avec ces tables à bien savoir manier les propriétés de symétrie ( =p(ε >1,5)) et de complémentarité (p(ε >1,5)=1- p(ε <1,5)) liées à la distribution de la variable normale.
Par convention et en accord avec la norme NFX 06-002*, on écrira que p(ε <ε i)=F(ε i) où F représente la fonction de répartition de la variable normale centrée réduite.
Selon cette norme, une fonction de répartition est une fonction de x, égale à la probabilité que la variable aléatoire X soit strictement inférieure à x : F(x)=p(X<x)
1.1.2.Loi Log-Normale (loi de Galton)
Une variable aléatoire X suit une loi Log-Normale si la variable suit une loi Normale.
Ce type de distribution se rencontre lorsque la variable aléatoire est soumise à de nombreux facteurs indépendants, dont aucun n'est prépondérant, mais dont les effets sont multiplicatifs. (ex : distribution de la taille des gouttes d'une émulsion).
La densité de probabilité est caractérisée par une courbe dissymétrique, étalée vers la droite.
Si l'on porte lnX au lieu de X, la courbe est alors symétrique et redevient une courbe en cloche.
1.1.3.Loi uniforme
Cette loi est définie sur un intervalle continu [0 ;a] de valeur réelle avec une fonction de densité de probabilité
Son espérance mathématique est E(X)= a/2 et sa variance est Var (X)= a2/12
