1.3.Modélisation (étude de la normalité) d'une distribution observée par la droite de Henry.

Revenons maintenant au cas pratique où nous disposons d'une série de donnée (correspondant à un échantillon) que nous avons décrit statistiquement. Plusieurs étapes ont été réalisées :

• description de la variable aléatoire étudiée

• regroupement éventuel des données en classes

• représentation graphique de la distribution observée

• calcul des principaux paramètres de position et de dispersion et estimation des paramètres de la population.

Nous disposons d'informations qui nous permettent maintenant d'analyser plus en détail la population d'où a été extrait l'échantillon. Nous pouvons en effet rechercher un modèle qui décrirait le mieux possible la distribution de la variable aléatoire étudiée.

Ainsi dans l'exemple du poids des nouveau-nés nous avions obtenu l'histogramme suivant :

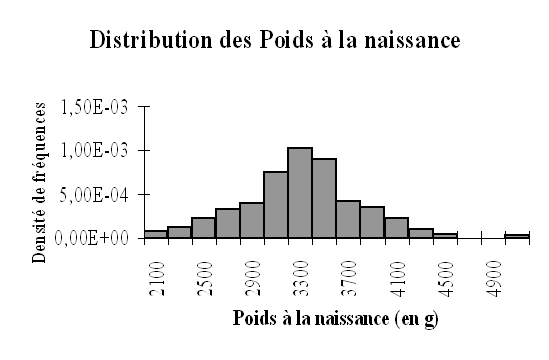
On remarque tout de suite à la forme de la distribution que la loi normale pourrait être un bon modèle théorique pour la distribution de cette variable continue. Nous allons essayer de vérifier cette hypothèse en utilisant une méthode graphique appelée droite de Henry.

Cette méthode d'ajustement graphique d'une loi normale à une distribution observée repose sur la relation linéaire qui existe entre la variable aléatoire X et la variable centrée réduite ε : peut en effet s'écrire aussi : . On remarquera qu'ici on a utilisé dans la formule les estimations de µ et σ car les paramètres de la population sont inconnus.

Si la distribution de X suit une loi normale, il existe donc une relation linéaire de la forme y=ax+b entre les variables x et ε  ; c'est l'équation de la droite de Henry.

Pour vérifier la linéarité, nous allons utiliser pour chaque valeur observée de X la fréquence relative cumulée de la classe correspondante. Cette fréquence cumulée correspond en effet au résultat de la fonction de répartition de la loi normale si la distribution suit bien une loi normale. A partir de la table de la loi normale (ou à l'aide d'un tableur), nous pouvons déterminer la valeur de la variable centrée réduite correspondant à chaque probabilité F(ε).

Si la distribution suit une loi normale on doit obtenir une droite en portant les extrémités de classe en abscisse et les valeurs de ε en ordonnée.

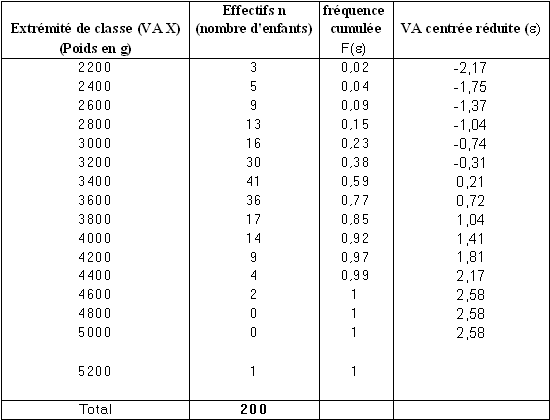
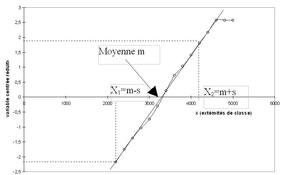
On constate que la distribution observée peut être assimilée à une loi normale car la linéarité est satisfaisante (hormis les 2 points supérieurs qui sont dus à des classes de même fréquence).

Cette droite coupe l'axe des abscisses à une valeur correspondant à la moyenne de la distribution. La pente de la droite est égale à 1/s et permet donc de déterminer l'écart type. On peut également déterminer l'écart type à partir des abscisses x1 et x2 correspondant respectivement aux ordonnées -2 et + 2. La différence x1-x2 est égale à 4 écart types et l'écart type est alors donné par .

Pour simplifier la procédure et éviter de calculer les écarts réduits, on peut utiliser du papier gausso-arithmétique, dont l'échelle des ordonnées est graduée non plus à partir des valeurs de la variable centrée réduite mais directement en probabilité (valeurs de F(ε )). L'échelle des ordonnées n'est alors plus linéaire et il suffit d'y placer les fréquences relatives cumulées observées dans l'échantillon.

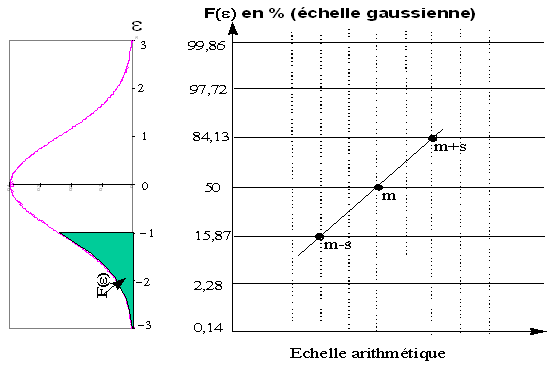
Cette méthode d'étude de la normalité d'une distribution s'adapte bien aux variables aléatoires continues. Il existe cependant d'autres moyens de vérifier la normalité d'une distribution observée qui sont basées sur des test statistiques (test du Khi 2 par exemple) que nous verrons par la suite. Ces tests présentent l'avantage de pouvoir préciser la normalité d'une distribution avec un pourcentage d'incertitude connu. Ils permettent également d'ajuster des distributions observées concernant des VA discrètes à des distribution théoriques discontinues (binômiale, poisson, hypergéomètrique...).

Un des intérêts pratiques de tels ajustements est de valider un modèle de distribution de la variable étudiée ce qui permet de démontrer par la suite que le phénomène étudié est stable (dans le temps par exemple). En effet, nous verrons que la normalité de la distribution de la variable aléatoire est une des conditions les plus fréquentes pour l'exécution d'un test statistique. Faire une hypothèse de normalité alors que ce n'est pas le cas, peut entraîner des conclusions totalement fausses. Il est donc utile de se donner les moyens de vérifier ou d'infirmer une telle hypothèse.