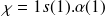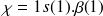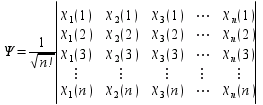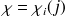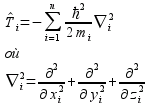Les équations de base
Ces méthodes sont basées sur la résolution des équations de la Physique Quantique (l'équation de Schrödinger).
Grâce à l'approximation de Born-Oppenheimer on peut traiter le mouvement des électrons en considérant l'ossature des noyaux fixe. On résout alors l'équation suivante :
Comme nous l'avons vu au début de ce chapitre,
est l'opérateur Hamiltonien,
la fonction d'onde et
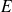l'énergie. Nous allons maintenant donner quelques bases permettant de donner une expression mathématique de ces différents termes.
Chaque électron « appartient » à une spinorbitale.
Une spinorbitale est une fonction qui prend en compte la répartition spatiale de l'électron (orbitale) + son spin.
Par exemple, pour l'électron n°1 d'une couche 1s dans un atome d'hydrogène :
La fonction spatiale 1s contient les nombres quantiques n, l, m
et
sont les fonctions associées au spin
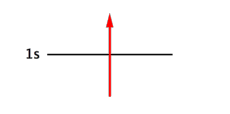 couche-1s-alphaInfo1 |
|
 couche-1s-betaInfo2 | ou
|
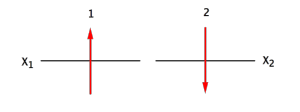
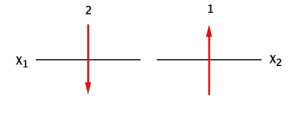
Cas d'un système à 2 électrons
|
|
-
Pourquoi le signe - ?
Parce que si
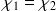, on a
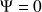, c'est le principe de Pauli.
-
Pourquoi
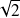?Pour normaliser et avoir une densité électronique totale
On peut alors re-écrire cette expression sous la forme d'un déterminant :
Dans le cas d'un système polyélectronique (n électrons), la fonction d'onde totale du système prend la forme d'un déterminant de Slater :
|  SpinorbitalesInfo5 |
Il contient toutes les informations concernant toutes les interactions agissant sur les électrons.
Ti est l'opérateur d'énergie cinétique pour les particules (noyaux ou électrons) de masse mi
Vij sont les opérateurs d'énergie potentielle (énergie électrostatique)
-
VNe : Noyaux – électrons
-
Vee : électrons – électrons
-
VNN : Noyaux - Noyaux
Ces opérateurs décrivent toutes les interactions entre les particules chargées de la molécule.
Dans l'approximation de Born Oppenheimer,
devient :
On calcule alors l'énergie de la manière suivante :
où
est le déterminant de Slater et
l'Hamiltonien précédemment décrits.
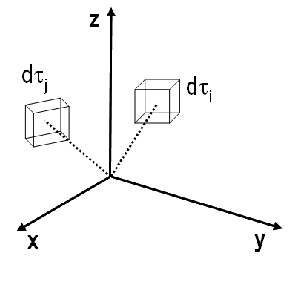
Le calcul de l'énergie revient à calculer un grand nombre d'intégrales qui correspondent chacune à une interaction donnée entre 2 électrons (intégrales bi-électroniques) ou entre 1 électron et 1 noyau.
Pour optimiser une structure (trouver la conformation et toutes les propriétés physico-chimiques correspondantes à cette conformation), il faut obtenir l'énergie minimum.
On calcule alors la dérivée de l'énergie, donnée par l'expression précédente, et on annule cette dérivée. On obtient les équations de Hartree-Fock.
