Les méthodes

Les méthodes ab initio sont basées sur la résolution complète des équations de Hartree-Fock, c'est-à-dire le calcul de tous les termes énergétiques et donc de toutes les intégrales. La méthode HF considère l'interaction électronique comme un champ moyen. C'est à dire que chaque électron ressent l'effet des autres électrons de façon moyenne (comme si les autres électrons formaient un nuage homogène d'électrons).

On peut alors choisir différentes fonctions mathématiques pour décrire les orbitales (STO 3G, 3-21G, 6-31G, 6-31G(d,p), 6-311++G(2d,p)).

L'ensemble de ces fonctions constitue la base.

Les spinorbitales moléculaires sont écrites comme des combinaisons linéaires des orbitales atomiques ( )

Les orbitales atomiques sont appelées fonctions de base, elles sont habituellement décrites par une combinaison linéaire de fonctions gaussiennes.

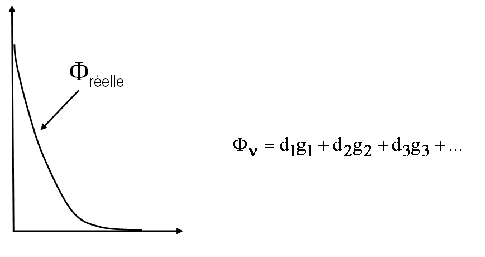
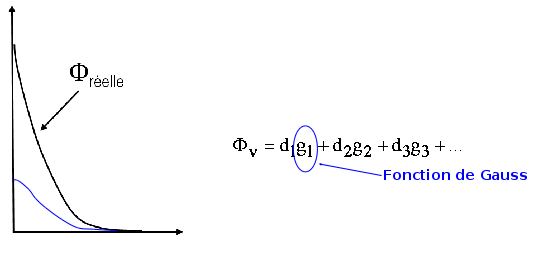
La base STO-3G contient 1 fonction de base décrite par 3 gaussiennes

La base 3-21G contient

• 1 fonction de base pour les états de cœur décrite par 3 gaussiennes

• 2 fonctions de base pour les états de valence décrites respectivement par 2 et 1 gaussiennes

La base 6-31G contient

• 1 fonction de base pour les états de cœur décrite par 6 gaussiennes

• 2 fonctions de base pour les états de valence décrites respectivement par 3 et 1 gaussiennes

La base 6-31G* (ou 6-31G(d)) contient en plus des fonctions de polarisation

La base 6-31+G contient en plus des fonctions diffuses

La base 6-311+G** (ou 6-311+G(d,p)) ...

Les méthodes HF peuvent être relativement fiables à condition de choisir une base suffisamment élaborée. De plus la méthode HF ne prend pas en compte les effets de corrélation électronique. Cette correction est souvent nécessaire pour améliorer la fiabilité des calculs et donner une meilleur reproduction de la réalité. La corrélation électronique est prise en compte dans les méthodes dites post-HF. Cependant ces méthodes nécessitent des temps de calcul très importants et ne peuvent être utilisées que pour des petites molécules.

Dans ce cas, on néglige ou on approxime certaines intégrales, c'est-à-dire certains types d'interaction.

Les simplifications :

• Choisir une base minimum :

  On ne prend que les orbitales de valence pour former la base

• Négliger certaines interactions à longue distance

• Utiliser des valeurs paramétrées pour les intégrales bi-électroniques restantes

Il existe ainsi de nombreuses méthodes semi-empiriques qui dépendent du nombre de simplifications (type d'interaction négligées) et des paramétrages : CNDO, NNDO, MNDO, AM1, PM3, SAM1.

La méthode AM1, développée en 1985, est la plus utilisée et donne souvent de très bons résultats pour un temps de calcul très réduit par rapport aux méthodes ab initio.

Comme nous l'avons dit précédent la méthode HF (et a fortiori les méthodes semi-empiriques) ne prennent pas en compte les effets importants de corrélations électroniques.

Les méthodes post-HF étant très coûteuses en temps de calcul, les méthodes DFT (Density Functional Theory) ont été développées pour prendre en compte ces effets.

Dans ce cas, les formalismes sont basés sur la densité électronique et l'énergie est :

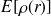
Les méthodes DFT sont relativement récentes mais sont de plus en plus utilisées, notamment en biologie. Elles sont moins coûteuses en temps de calcul que les méthodes post-HF et peuvent apporter une très bonne fiabilité pour certains systèmes moléculaires (e.g., compréhension des activités antioxydantes des polyphénols).