Signification des paramètres de régression
-
On cherche à savoir si la pente est significativement différente de 0 (droite horizontale)
-
Test de comparaison d’une valeur moyenne expérimentale et d’une valeur théorique : test de conformité de Student
-
Hypothèse
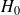 : a = 0 (la pente est nulle)
: a = 0 (la pente est nulle) -
Calcul de la valeur
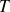
-
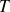 suit une loi de Student à
suit une loi de Student à
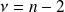 ddl
ddl -
Pour un risque
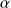 , on cherche la valeur seuil
, on cherche la valeur seuil
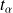 dans la table de Student :
dans la table de Student : -
Si
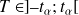 :
:
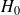 ne peut pas être rejetée (pente non significativement différente de 0)
ne peut pas être rejetée (pente non significativement différente de 0) -
Si
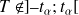 :
:
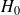 est rejetée au risque
est rejetée au risque
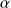 (
(
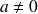 )
)
-
On cherche à savoir si l'ordonnée à l'origine est significativement différente de 0 (la droite passe par le point (0 ; 0))
-
Test de comparaison d’une valeur moyenne expérimentale et d’une valeur théorique : test de conformité de Student
-
Hypothèse
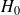 : b = 0 (l'ordonnée à l'origine est nulle)
: b = 0 (l'ordonnée à l'origine est nulle) -
Calcul de la valeur
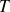
-
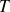 suit une loi de Student à
suit une loi de Student à
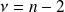 ddl
ddl -
Pour un risque
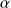 , on cherche la valeur seuil
, on cherche la valeur seuil
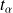 dans la table de Student :
dans la table de Student : -
Si
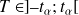 :
:
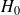 ne peut pas être rejetée (ordonnée à l'origine non significativement différente de 0)
ne peut pas être rejetée (ordonnée à l'origine non significativement différente de 0) -
Si
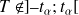 :
:
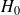 est rejetée au risque
est rejetée au risque
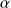 (
(
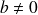 )
)
-
On peut éventuellement tester l’égalité des paramètres de régression avec une valeur particulière non nulle :
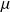
-
Hypothèse
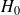 : a = µ (ou, le cas échéant, b = µ)
: a = µ (ou, le cas échéant, b = µ) -
Calcul de la valeur
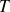
ou
-
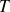 suit une loi de Student à
suit une loi de Student à
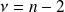 ddl
ddl -
Pour un risque
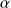 , on cherche la valeur seuil
, on cherche la valeur seuil
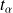 dans la table de Student :
dans la table de Student : -
Si
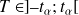 :
:
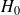 ne peut pas être rejetée (
ne peut pas être rejetée (
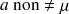 ou
ou
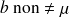 )
) -
Si
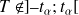 :
:
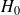 est rejetée au risque
est rejetée au risque
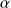 (
(
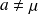 ou
ou
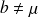 )
) -
Exemple :
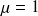 à comparer à
à comparer à
 (pente parallèle à 1e bissectrice ?)
(pente parallèle à 1e bissectrice ?)
-
On cherche à savoir si le coefficient de corrélation est significativement différent de 0 (X et Y non indépendants)
-
Test de comparaison d’une valeur moyenne expérimentale et d’une valeur théorique : test de conformité de Student
-
Hypothèse
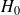 : r = 0 (X et Y indépendants)
: r = 0 (X et Y indépendants) -
Calcul de la valeur
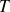
-
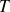 suit une loi de Student à
suit une loi de Student à
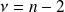 ddl
ddl -
Pour un risque
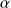 , on cherche la valeur seuil
, on cherche la valeur seuil
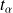 dans la table de Student :
dans la table de Student : -
Si
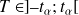 :
:
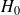 ne peut pas être rejetée (
ne peut pas être rejetée (
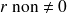 )
) -
Si
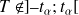 :
:
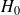 est rejetée au risque
est rejetée au risque
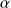 (
(
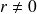 : X et Y corrélés)
: X et Y corrélés)
-
On cherche à comparer
 à une valeur non nulle
à une valeur non nulle
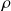
-
Test de conformité
-
Hypothèse
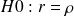
-
Calcul de la valeur
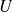
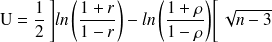
-
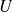 suit une loi de normale centrée réduite
suit une loi de normale centrée réduite -
Pour un risque
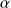 , on cherche la valeur seuil
, on cherche la valeur seuil
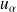 dans la table de la loi normale :
dans la table de la loi normale : -
Si
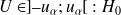 ne peut pas être rejetée (
ne peut pas être rejetée (
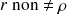 )
) -
Si
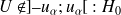 est rejetée au risque \alpha (
est rejetée au risque \alpha (
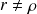 )
) -
Cas particulier :
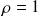 (tous les points sont alignés sur la courbe)
(tous les points sont alignés sur la courbe)
