Test d'homogénéité - Test d'indépendance - Introduction
Comparaison de la distribution d’une variable qualitative dans plusieurs échantillons : test d’homogénéité.
-
Un facteur A peut prendre k valeurs différentes sur une population
-
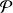
La probabilité d’apparition des différentes valeurs de A :
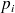(avec
) -
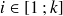Soit m échantillons
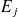de tailles respectives
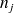issu de
-
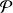
Les fréquences d'apparition des valeurs de A dans
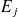sont notées
-
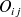
test d'indépendance
-
Un facteur A peut prendre k valeurs différentes et un facteur B peut prendre m valeurs différentes sur une même population
-
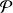
La probabilité d’apparition des différentes valeurs de A :
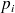(avec
) -
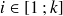Probabilité d’apparition des différentes valeurs de B :
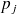(avec
) -
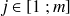Soit un échantillon
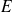de taille n issu de
-
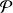
Les fréquences d'apparition simultanée des valeurs de A et de B dans
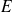sont notées
-
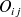
Hypothèse
:
-
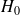Les différences observées entre tous les échantillons sont le fait du hasard (test d’homogénéité).
-
ou : les facteurs A et B sont indépendants (test d’indépendance).
Hypothèse
:
-
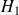Les distributions observées diffèrent entre-elles.
