Les différents dénombrements
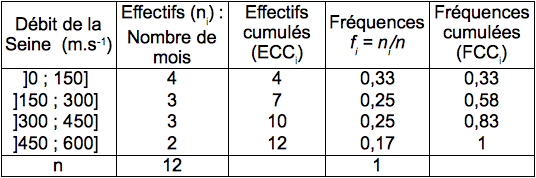
Le dénombrement des individus par classe peut être défini de plusieurs façons :
nombre d'individus appartenant à une classe.
Il est généralement noté
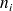. La somme des effectifs de toutes les classes est la taille de l'échantillon
.
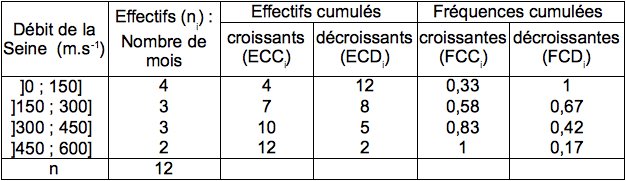
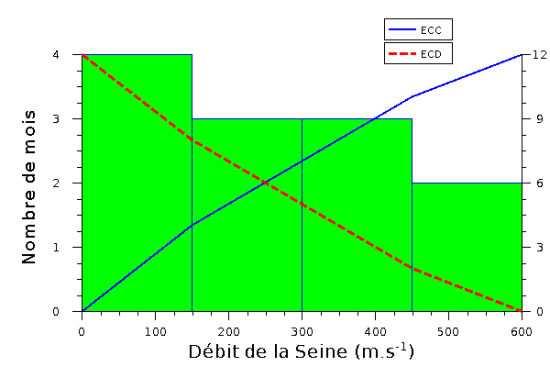
somme des effectifs de la classe étudiée et des effectifs des classes qui lui sont inférieures.
L'effectif cumulé de la dernière classe vaut
(c'est-à-dire la somme des
).
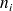rapport entre la taille de la classe étudiée et la taille de l'échantillon.
Nous étudions dans ce cas l'importance de la classe par rapport à la globalité de l'échantillon. La somme de toutes les fréquences est égale à 1. Elle est notée
.
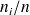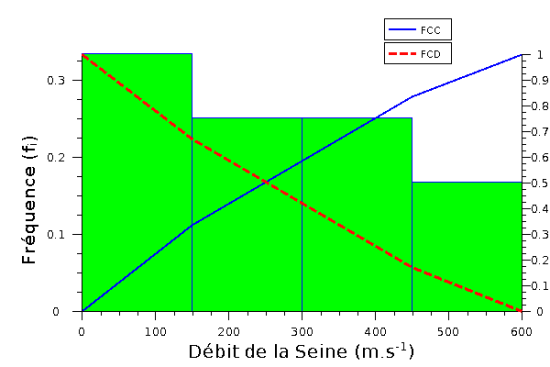
somme des fréquences de la classe étudiée et des fréquences des classes qui lui sont inférieures.
On distingue :
-
les fréquences cumulées croissantes : la fréquence cumulée de la dernière classe vaut 1.
-
les fréquences cumulées décroissantes : la fréquence cumulée de la première classe vaut 1.
souvent employée pour que la surface de chaque rectangle de l'histogramme corresponde à la fréquence relative de la classe. Cette notion est notamment employée dans la construction d'histogrammes à partir des classes de valeurs d'amplitudes inégales.
