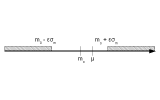
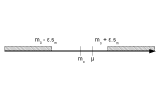
estimation de la moyenne µ d'une population
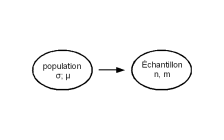 estimation d'une moyenneInfo1 |
2° cas :
L'écart type estimé de la moyenne est :
Si n 30, µ appartient à l'intervalle de confiance [(mo - .sm) ;(mo + .sm)] avec un risque correspondant à choisi. Si n < 30 (petit effectif) et si la Variable Aléatoire suit une loi normale, µ appartient probablement à l'intervalle [(mo – t. sm) ;(mo + t .sm)] où t est le coefficient de Student donné dans les tables et correspondant à un risque et un nombre de degrés de liberté = n-1. Par exemple, pour n = 11 : = n-1 = 10, nous trouvons : au risque de 5%, t = 2,228 # 2,23 au lieu de = 2 au risque de 1%, t = 3,169 # 3,17 au lieu de = 2,6. | 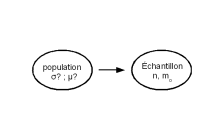 Estimation d'une moyenneInfo2 |