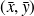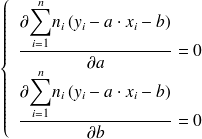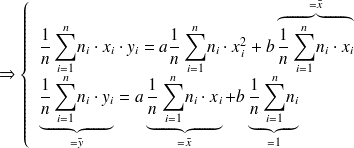Régression linéaire - Les moindres carrés
Si le modèle s’applique parfaitement aux points expérimentaux, on a
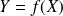
Généralement, ce n’est pas le cas, on a donc :
(
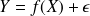
est l’écart entre la valeur expérimentale et la valeur calculée)
On pose alors
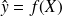
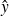est la valeur de
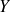calculée par la droite pour l’abscisse
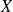
donc :
-
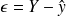
Pour le modèle idéal, on aurait :
-
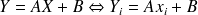
A : pente vraie de la droite (généralement inconnue)
-
B : ordonnée à l'origine vraie de la droite (généralement inconnue)
-
-
Pour la droite expérimentale, on a :
-
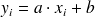
a : estimation de la pente vraie A
-
b : estimation de l'ordonnée à l'origine vraie B
-
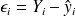: différence entre la valeur expérimentale de
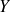et la valeur calculée par l’équation de la droite pour l’abscisse
-
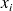
Soient deux variables
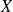et
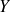étudiées sur une population
-
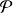
Soit un nuage de n points
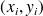avec les effectifs respectifs
-
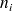
Choix d’une fonction mathématique suggérant une relation fonctionnelle entre
et
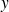(basé sur l’allure du nuage de points et des considérations sur le phénomène étudié) -
Calcul de la valeur
-
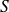
Avec, si on prend l'exemple d'une droite de régression :
-
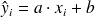
On cherche alors
et
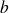qui rendent minimum la valeur de
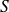soit :
-
Lorsque
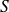est minimum, la dérivée première (par rapport à
et à
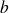) est égale à
-
et
Avec les dérivées partielles de
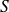par rapport à
et à
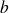, on obtient le système d’équations suivant :
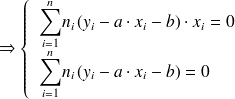
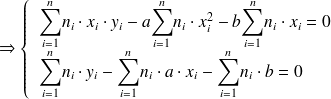
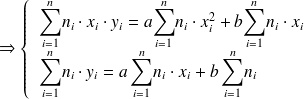
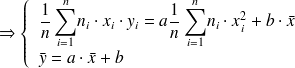
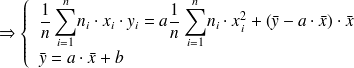
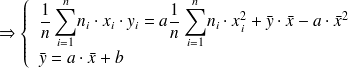
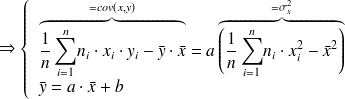
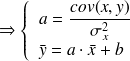
La droite passe donc par le point moyen G de coordonnées :
