Les mesures de la tendance centrale
est la mesure de la tendance centrale la plus facile à calculer.
Elle est obtenue par la division de la somme de toutes les valeurs de l'échantillon par la taille de l'échantillon (
). Cette mesure est sensible aux valeurs extrêmes.
La moyenne expérimentale d'un échantillon de n valeurs
est définie comme la moyenne arithmétique de ces valeurs ; on la note souvent
.
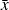Avec la série : 12, 3, 24, 1, 5, 8, 7, qui comporte n = 7 valeurs, on obtient :
détermine la valeur la plus fréquente dans un échantillon.
Si l'échantillon est divisé en classes, la classe modale constitue la classe la plus fréquente.
Dans l'exemple ci-dessous, la classe modale est la classe ]0 ; 150], et contient 4 mois.
est la valeur telle que 50 % des observations de l'échantillon lui sont inférieures.
-
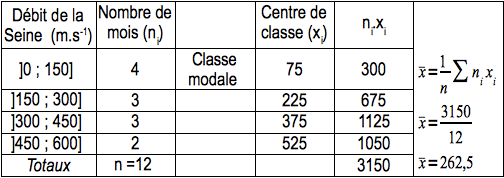
Si le nombre d'observations est pair : la médiane est la moyenne entre les observations
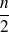et
. -
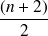Si le nombre d'observations est impair : la médiane est la valeur
.
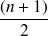Dans l'exemple précédent (Tableau 9), l'échantillon est composé de 12 mois. Cela implique que la médiane se trouve entre la 6e et la 7e valeur. La médiane est donc dans la classe ]150 ; 300].
Soit la série 12, 3, 24, 1, 5, 8, 7
on l'ordonne : 1, 3, 5, 7, 8, 12, 24,
7 est la médiane de la série
Soit la série 12, 3, 24, 1, 5, 8, 7, 6
on l'ordonne : 1, 3, 5, 6, 7, 8, 12, 24,
6,5 est la médiane de la série
