Les mesures de dispersion
Pour une population statistique d’effectif n dont la moyenne de la population µ est connue par théorie ou par hypothèse, on utilise la formule suivante :
Cette formule est simplifiable :
L'écart-type de la population, noté
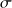, est défini par :
La variance expérimentale d'un échantillon
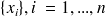est donnée par
On divise par
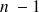et non par
. Ceci pour que la variance expérimentale soit un bon estimateur de la variance théorique (celle de la population donc de
).
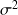Une autre expression de
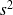, équivalente :
L'écart-type expérimental, noté
, est défini par
Différence entre la plus grande valeur et la plus petite dans une série statistique
soit la série 12, 3, 24, 1, 5, 8, 7
L’étendue est 24 – 1 = 23
-
les quartiles : Q1, Q2 = médiane, Q3 (4 classes avec 25% de l’effectifs total)
-
Écart interquartile : Q3 - Q1
-
-
les quintiles R1, R2, R3, R4 (5 classes avec 20% de l’effectif total)
-
Les déciles D1, D2, ..., D9 (10 classes avec 10% de l’effectif total)
-
Les centiles C1, C2, ..., C99 (100 classes avec 1% de l’effectif total)
-
On les détermine de la même manière que la médiane.
