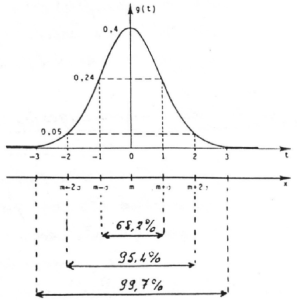
L'Ecart Réduit

On peut ainsi déterminer la probabilité que la variable centrée réduite t appartienne à l'intervalle [t1, t2]. Ainsi d'une population gaussienne de moyenne m et d'écart type , nous pouvons déduire le pourcentage de ses éléments dont l'écart réduit est inférieur à 1, 2, 3. Ainsi 68,2% ont un écart réduit inférieur à 1, etc ....(voir figure)

Prenons le cas t=2, l'intervalle [(m-2), (m+2)[ est appelé intervalle de confiance (ou de pari) au coefficient de sécurité de 95,4%. A cet intervalle de confiance est attaché un risque de (100-95,4)% = 4,6% ≈ 5%.

La loi de Gauss s'applique plus particulièrement lorsque la probabilité p d'un événement A est telle que p ≥ 0,1 ou ≤ 0,9 et si le nombre n d'épreuves est tel que la moyenne np et nq  5, avec n  30.

(La loi normale de Gauss est une approximation de la loi Binomiale si n >30 et np et nq > 5 ; de la loi de Poisson si n > 30 et np = m > 15).