ANOVA à un facteur - Schématisation de l'analyse multiple de moyennes

Figure 38 : Expériences avec plusieurs échantillons[Zoom...]

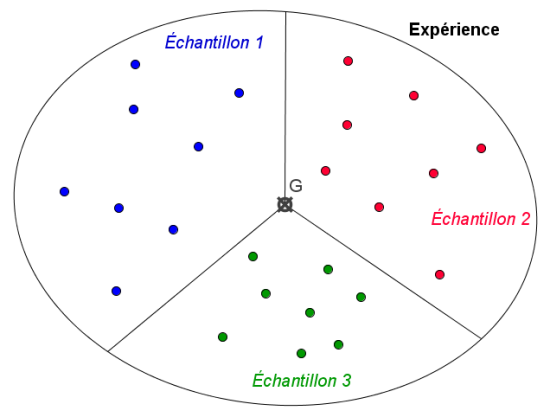
• Soit une Expérience faisant intervenir k échantillons de 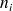individus.

• Le nombre total d'individus est

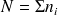
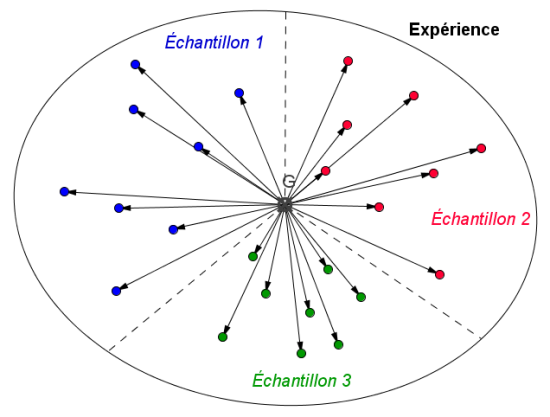
• On calcule la moyenne générale des mesures de l'expérience (G).

Figure 39 : Variabilité totale (toutes les échantillons confondus)[Zoom...]

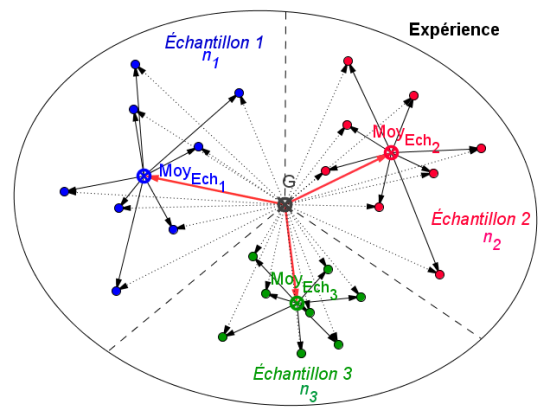
• Variabilité totale au sein de l'expérience (quel que soit l'échantillon) : reflète les écarts de tous les individus par rapport à la moyenne générale (G) de l'expérience.

• Calcul de la Somme des Carrés des Écarts à la moyenne totale ( ).

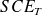• Degrés de liberté (DDL) associés : N-1.

Figure 40 : Effet du facteur étudié sur les moyennes des échantillons par rapport à la moyenne générale[Zoom...]

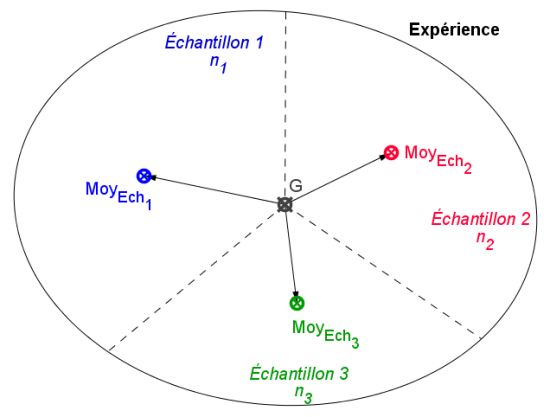
• Variabilité factorielle : reflète les écarts des moyennes des échantillons (supposées influencées par le facteur étudié) par rapport à la moyenne générale (G) de l'expérience.

• Calcul de la Somme des Carrés des Écarts à la moyenne factorielle ( ).

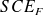• DDL associés : k-1.

Figure 41 : Variabilité intragroupe (résiduelle)[Zoom...]

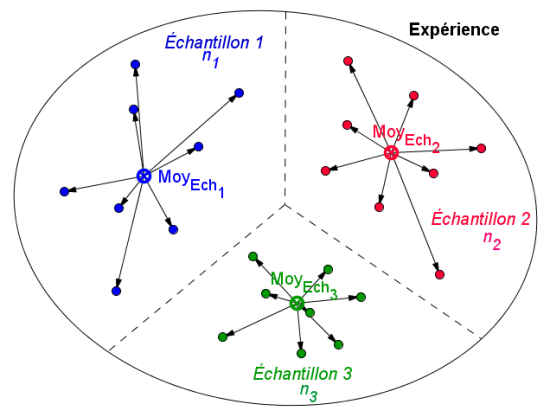
• Variabilité résiduelle (liée à l'individu) : reflète l'importance des variations individuelles dans chaque échantillon.

• Calcul de la Somme des Carrés des Écarts à la moyenne résiduelle ( ).

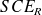• DDL associés : N-k.

Figure 42 : Représentation combinée de toutes les sources de variabilités[Zoom...]

Pour résumer :

• 

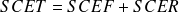
• DDL associés : N-1 = k-1 + N-k.

• On comparera les variabilités factorielle 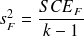et résiduelle

Figure 43 : Représentation schématique d'un effet factoriel peu marqué

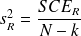
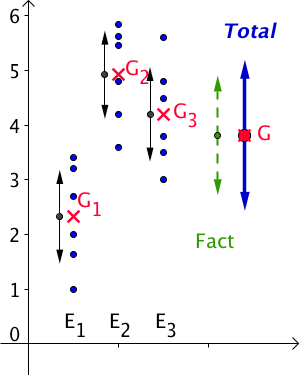
• Effet du facteur : faible

• Variation Factorielle : grande (légèrement supérieure à la variation Résiduelle)

• Variation Résiduelle : grande

Figure 44 : Représentation schématique d'une variabilité factorielle non significative

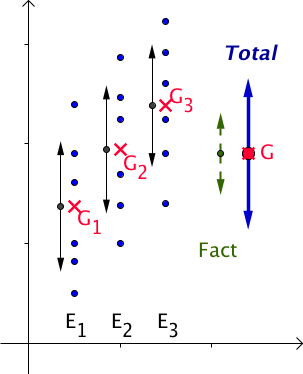
• Effet du facteur : non significatif

• Variation Factorielle : faible (inférieure ou égale à la variation Résiduelle)

• Variation Résiduelle : grande

Figure 45 : Représentation schématique d'un effet factoriel significatif

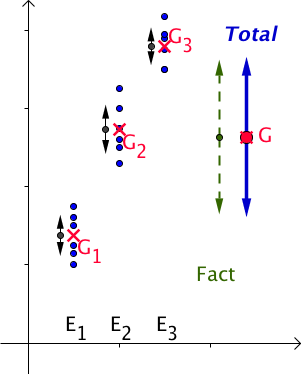
• Effet du facteur : significatif

• Variation Factorielle : grande (très supérieure à la variation Résiduelle)

• Variation Résiduelle : faible