ANOVA à deux facteurs - Introduction
-
Étude simultanée d’un facteur A à p modalités et d’un facteur B à q modalités.
-
Pour chaque couple de modalités (A, B) :
-
On a un échantillon
(
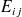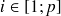et
). -
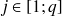Tous les
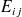sont de mêmes tailles
.
-
-
les populations étudiées suivent une distribution normale
-
les variances des populations sont toutes égales (HOMOSCEDASTICITE)
-
les échantillons
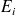de tailles
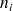sont prélevés aléatoirement et indépendamment dans les populations.
-
Déterminer si les échantillons varient de la même manière.
-
Si nous démontrons l'homogénéité des variances, alors nous pouvons comparer les moyennes de ces échantillons.
Test de l'homogénéité des variances
-
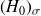: les variances sont homogènes -
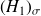: Au moins une des variances est différente des autres→ utilisation d'un test de comparaison de plusieurs variances
Conclusion
-
Si
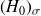est rejetée : il est théoriquement impossible de comparer des échantillons qui ne varient pas de la même manière. -
Si
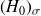n’est pas rejetée : par conséquent, il est possible de comparer les moyennes de tels échantillons
