ANOVA à deux facteurs - Cas particulier où n = 1 :
-
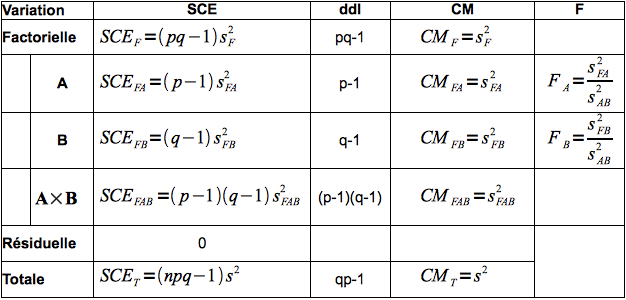
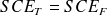
Si
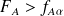=> rejet de
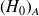au risque
:-
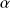La variance factorielle est significativement supérieure à la variance résiduelle : les moyennes diffèrent significativement entre-elles.
→ on attribue une influence significative au facteur A étudié.
-
-
Si
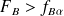=> rejet de
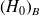au risque
:-
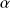La variance factorielle est significativement supérieure à la variance résiduelle : les moyennes diffèrent significativement entre-elles.
→ on attribue une influence significative au facteur B étudié.
-
-
Le test pour
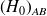n'est pas réalisable
-
Recherche du degré de signification p pour chaque test (recherche du risque
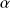le plus petit possible pour conclure au rejet de
)
-
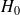Sinon rien ne permet de dire que les moyennes des populations ne sont pas égales =>
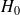n’est pas rejetée.
