Notions d'interpolation et d'extrapolation
L'interpolation est un calcul qui consiste à estimer la valeur inconnue d'une des deux variables étudiées. Ce calcul est réalisé dans le domaine d'étude fourni par l'échantillon en utilisant le modèle mathématique obtenu.
Ce calcul est a priori toujours valable à partir du moment où le modèle représente correctement le phénomène étudié.
-
Calcul d'une valeur de y
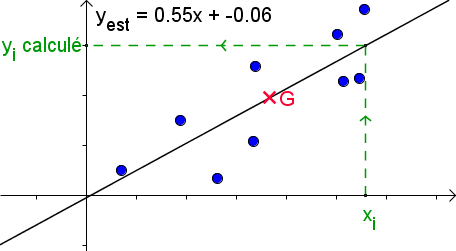
Dans cet exemple : grâce au modèle on estime la valeur de la variable dépendante (
) pour un x particulier (
).
-
Calcul d'une valeur de x
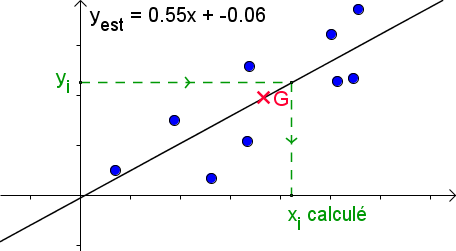
Dans cet exemple : grâce au modèle, à partir d'une valeur connue de
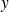, on pourra estimer la valeur
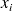correspondante.
L'extrapolation est un calcul qui consiste également à estimer la valeur inconnue d'une des deux variables étudiées. Contrairement à l'interpolation, ce calcul est réalisé en dehors du domaine d'étude fourni par l'échantillon en utilisant le modèle mathématique obtenu.
Ce calcul peut être contestable dans la mesure où le modèle calculé n'est réellement applicable que dans le domaine d'étude. En dehors de cet intervalle, rien ne prouve que le modèle mathématique retenu soit toujours valable.
On par exemple envisager deux cas de figure :
-
Extrapolation : calcul de y « acceptable »
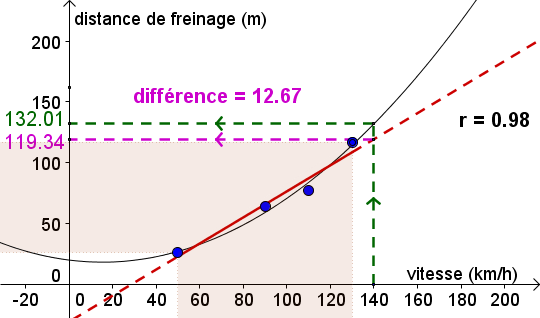
Dans cet exemple : grâce au modèle, on cherchera à extrapoler les résultats (estimation des valeurs en dehors du champs d'étude). Cette extrapolation est « acceptable » dans ce cas précis car l'erreur commise est relativement faible.
-
Extrapolation : calcul de y « aberrant »
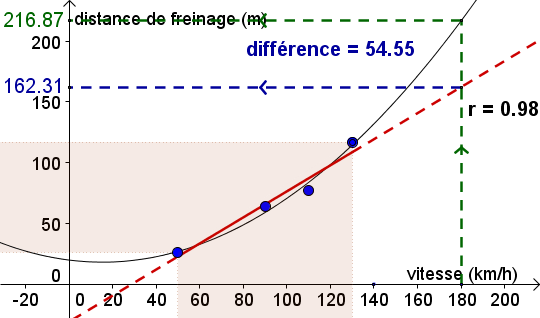
Dans cet exemple : l'extrapolation est « aberrante » dans ce cas précis car l'erreur commise est assez élevée. La droite s'écarte très rapidement de la parabole du modèle « vrai ».
